Relativistic Mass: Meaning, Theory, Formula, Examples, and Modern Perspective
Introduction
In classical Newtonian physics, mass is considered an invariant quantity—a fixed property of an object that does not change regardless of how fast the object moves. However, the advent of Albert Einstein’s Special Theory of Relativity (1905) fundamentally altered this understanding. One of the most debated and fascinating outcomes of this theory is the concept of relativistic mass, which suggests that the mass of an object increases as its velocity approaches the speed of light.
The idea of relativistic mass played a significant role in early explanations of relativistic motion and energy. Although modern physics prefers alternative formulations, understanding relativistic mass remains important for grasping how motion, energy, and spacetime interact at extreme speeds.
What Is Relativistic Mass?
Relativistic mass is the mass of an object when it is moving at a velocity comparable to the speed of light. According to special relativity, as an object’s speed increases, its resistance to acceleration also increases. This effect can be interpreted as an increase in mass.
In simple terms:
The faster an object moves, the heavier it becomes (from the perspective of an observer at rest).
This increase is negligible at everyday speeds but becomes extremely significant as the object approaches the speed of light.
Rest Mass vs Relativistic Mass
To understand relativistic mass clearly, it is essential to distinguish between two types of mass:
1. Rest Mass (Invariant Mass)
- Denoted as m₀
- The mass of an object measured when the object is at rest relative to the observer
- Does not change, regardless of the object’s speed
- Considered a fundamental property of matter
2. Relativistic Mass
- Denoted as m
- The mass of an object when it is moving relative to the observer
- Increases with velocity
- Depends on the observer’s frame of reference
Mathematical Formula of Relativistic Mass
The relativistic mass is given by the equation:
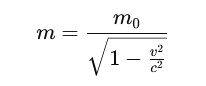
Where:
- m = relativistic mass
- m₀ = rest mass
- v = velocity of the object
- c = speed of light in vacuum (≈ 3 × 10⁸ m/s)
Understanding the Formula
- When v ≪ c (very small compared to the speed of light), the denominator is nearly 1, so:
m≈m0
This explains why relativistic effects are not noticeable in everyday life. - As v → c, the denominator approaches zero, causing m → ∞.
This implies that an infinite amount of energy would be required to accelerate an object with mass to the speed of light.
Physical Interpretation of Relativistic Mass
The increase in relativistic mass can be understood as:
- Increased inertia: The object becomes harder to accelerate.
- Increased energy content: Kinetic energy contributes significantly to the object’s total energy.
- A manifestation of spacetime geometry rather than a literal “weight gain.”
This interpretation explains why particles in accelerators require enormous energy for even tiny increases in speed at near-light velocities.
Relativistic Mass and Energy
Einstein’s famous equation:
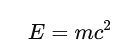
can be interpreted in two ways:
- Using relativistic mass:
- Total energy equals relativistic mass multiplied by ( c^2 )
- Using rest mass (modern approach):
- Total energy includes rest energy and kinetic energy:
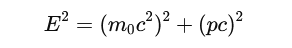
Here, p is relativistic momentum.
This shows that what was once attributed to “mass increase” can also be explained by increasing energy and momentum.
Relativistic Mass in Particle Physics
Relativistic mass is especially relevant in high-energy physics:
- Electrons in particle accelerators (like the Large Hadron Collider) exhibit extreme relativistic effects.
- Their effective inertia increases dramatically as they approach the speed of light.
- This prevents massive particles from ever reaching light speed.
Photons, however:
- Travel at the speed of light
- Have zero rest mass
- Still carry energy and momentum
- Do not have relativistic mass in the traditional sense
Why Objects Cannot Reach the Speed of Light
The concept of relativistic mass explains a fundamental cosmic limit:
- As velocity increases, relativistic mass increases.
- More force is required for further acceleration.
- At the speed of light, mass would become infinite.
- Infinite energy is physically impossible.
Hence, no object with rest mass can reach or exceed the speed of light.
Relativistic Mass vs Modern Physics View
Traditional (Older) View:
- Mass depends on velocity.
- Relativistic mass is a useful concept for explaining inertia.
Modern Physics View:
- Mass is invariant (rest mass only).
- Velocity dependence is assigned to energy and momentum, not mass.
- Relativistic mass is often avoided in textbooks to prevent confusion.
Despite this, relativistic mass is still:
- Historically important
- Pedagogically useful
- Occasionally used in popular science explanations
Advantages and Criticisms of Relativistic Mass
Advantages:
- Provides intuitive explanation for resistance to acceleration
- Historically aligns with early interpretations of relativity
- Useful in certain educational contexts
Criticisms:
- Can confuse mass with energy
- Not Lorentz-invariant
- Less consistent with modern relativistic formalism
Everyday Example (Conceptual)
Consider pushing a cart:
- At low speeds, it accelerates easily.
- At near-light speeds (hypothetically), it resists acceleration enormously.
- This resistance can be interpreted as an increase in relativistic mass.
In real life, such speeds are impossible for macroscopic objects, which is why we don’t observe this effect directly.
Summary
- Relativistic mass increases with velocity and becomes infinite at the speed of light.
- It arises from Einstein’s Special Theory of Relativity.
- The concept explains why massive objects cannot reach light speed.
- Modern physics prefers invariant mass and energy-based formulations.
- Despite declining usage, relativistic mass remains a valuable conceptual tool.
Conclusion
Relativistic mass represents a crucial stepping stone in the evolution of modern physics. While contemporary approaches emphasize invariant mass and relativistic energy-momentum relationships, the concept of relativistic mass provides deep insight into how motion at extreme speeds reshapes our understanding of matter, energy, and the limits of the universe. Understanding it not only honors the historical development of relativity but also strengthens conceptual clarity about why the universe enforces a universal speed limit—the speed of light.

